მეორე კოსმოსური სიჩქარისა და გრავიტაციული მანევრის შესახებ

 რა არის მეორე კოსმოსური სიჩქარე?

 ჩვენს მიერ ზემოთ აგდებული ქვა 5 – 10 მეტრ სიმაღლეს აღწევს, ჩერდება და უკან ვარდება. მას დედამიწა იზიდავს, ამუხრუჭებს, მეტი აჩქარების მინიჭება კი ჩვენს კუნთებს არ შეუძლია. თუ ზარბაზნიდან გავისვრით, ქვა გაცილებით მაღლა აიჭრება (50 კმ-ზეც კი), თუმცა, მაინც უკან, დედამიწის ზედაპირზე ჩამოვარდება. მეორე კოსმოსური სიჩქარე კი არის სიჩქარე, რომლითაც ქვა უნდა გავისროლოთ, რათა მან დედამიწის მიზიდულობა დაძლიოს და შორს გაფრინდეს. მაგრამ, სანამ ის მიფრინავს, დედამიწა მიზიდულობით ამუხრუჭებს და სიჩქარეს უმცირებს მას! შეიძლება ითქვას, რომ შორს გაფრენილი ქვა გაჩერდება. ასე რომ, რა სიჩქარით მოგვიწევს გაფრენა, მაგალითდ, სატურნისკენ, იმაზე იქნება დამოკიდებული, თუ რამდენად აჭარბებდა ჩვენი სასტარტო სიჩქარე, მეორე კოსმოსურ სიჩქარეს.

 არ არსებობს ზარბაზანი, რომელიც ჭურვს 11,2 კმ/წმ (40 000 კმ/სთ.). სიჩქარეს მიანიჭებს! სწორედ ამიტომ იყო კოსმოსური ფრენები შეუძლებელი, რაკეტების გამოჩენამდე. სტარტისთანავე რაკეტის მაქსიმალურად აჩქარება საჭირო არ არის, ის თანდათან უმატებს, საწვავის წვითა და მოძრაობის საპირისპირო მხარეს გატყორცნით. რაკეტის აფრენის ვიდეო ჩანაწერს თუ ნახავთ, მიხვდებით, რომ სტარტისას არანაირი მაღალი სიჩქარე არ არის (მით უმეტს მეორე კოსმოსური სიჩქარე). პატარა კოსმოსური აპარატის ორბიტაზე გასატანადაც კი რაკეტა უზარმაზარი რაოდენობით სწვავს წვავს. ამის მერე, აპარატი ინერციით აგრძელებს ფრენას, ძრავების ჩართვის გარეშე.

 სატურნამდე მისაღწევად მარტო დედამიწის მიზიდულობის დაძლევა საკმარისი არ არის – მზის მიზიდულობაც უნდა დავძლიოთ! მზიდან დაშორებასთან ერთად, როგორც დედამიწის შემთხვევაში, სიჩქარე შემცირებას დაიწყებს – მის შესანარჩუნებლად ძრავების მუდმივი მუშაობა იქნებოდა საჭირო, ამდენი საწვავი კი კოსმოსურ აპარატზე უბრალოდ არ არის.

 ამრიგად, კოსმოსური აპარატის საჭირო ორბიტამდე გასატანად, რაკეტა-მატარებელი თავისი ძრავებით აჩქარებს მას; საწვავი იწვება, ამაჩქარებელი საფეხურები ერთმანეთის მიყოლებით ცვივა და მხოლოდ პატარა აპარატიღა რჩება, სამანევროდ საჭირო საწვავის მცირე რაოდენობით. აპარატი ინერციით აგრძელებს ფრენას და მზიდან დაშორებასთან ერთდ, მისი სიჩქარე მცირდება… ამასთან ერთდ, ის არა წრფივად, არამედ, როგორც სხვა პლანეტები, კომეტები და ყველაფერი, რაც მზის სისტემაშია – ელიფსის რკალის გასწვრივ მოძრაობს.

 რატომ ასე? და არა ზუსტად მზის მოპირდაპირე მიმართულებით? იმიტომ, რომ სიჩქარსითვის ბრძოლაში ძალიან ძლიერი პარტნიორი გვყავს – ჩვენი პლანეტა. ის ხომ მზის გარშემო 30 კმ/წმ. სიჩქარით მოძრაობს – მასთან ერთდ კი ყველა ჩვენ და ჩვენი კოსმოსური ხომალდები! ეს სიჩქარე დედამიწის ორბიტის გასწვრივ არის მიმართული, მზისკენ მიმართულების პერპენდიკულარულად. ზუსტად საწინააღმდეგოდ რომ გვემოძრავა, ეს სიჩქარე უნდა ჩაგვეხშო, რაც ზედმეტსა და უაზრო დანახარჯს მოითხოვდა. პირიქით, ეს სიჩქარე საჩვენოდ უნდა გამოვიყენოთ, ამაჩქარებელი რაკეტით მიღწეულ სიჩქარესთან დამატებით. ამიტომ, რაკეტა სწორედ იქეთ უნდა მივმართოთ, საითაც დედამიწა გადაადგილდება.

 სატურნამდე მიღწევა თუ ასეთი ძნელია, იუპიტერთან და მით უმეტეს ვენერასთან, რომელიც სულ სხვა მხარეს არის, მისვლა რატომ არის აუცილებელი? სატურნთან და მის იქეთ მოხვედრილ ყველა აპარატს, იუპიტერთან მისვლა მოუწია. არა ინტერესის გამო, არამედ საფრენი დროის შესამცირებლად. იუპიტერთან მისვლა გზას გვიმოკლებს, რადგან ის აჩქარებაში გვეხმარება!

 როგორ აჩქარებს იუპიტერი მის ახლოს მფრენ აპარატებს?

 წარმოიდგინეთ დრეკადი ბურთი, რომელიც უძრავ კედელს ეხლება. რა სიჩქარე ექნება მას კედლიდან არეკვლის მერე? რა თქმა უნდა, იგივე. თუ მისკენ მოძრავ კედელს დაეჯახება?

 ეს ყველაფერი, კედელზე მჯდომი ჭიანჭწველას თვალსაწიერიდან წარმოვიდგინოთ. კედელი თანამბრად მოძრაობს და ჭიანჭველას ჰგონია, რომ ისიც და კედელიც გაჩერებულია. ამას გალილეისეული ფარდობითობა ჰქვია: თუ წრფივად და თანაბრად ვმოძრაობთ, ფიზიკის ყველა კანონი ისეთივე მართებული იქნება ჩვენთვის, როგორც უძრავად ყოფნის დროს.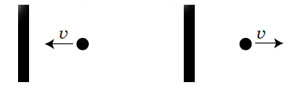

 ჭიანჭველა ხედავს, რომ მისკენ ბურთი მიფრინავს. რა სიჩქარით? თუ ჩვენ მიმართ ბურთის სიჩქარე იყო v, ხოლო კედლის სიჩქარე u, ბურთი v + u სიჩქარით უახლოვდება ჭიანჭველას. ჭიანჭველასთვის ყველაფერი ისე ჩანს, თითქოს უძრავ კედელზე იჯდეს; შეჯახება, და ბურთი იგივე v + u სიჩქარით აირეკლება. ახლა კი ჩვენთან დაკავშირებულ ათვლის სისტემაზე გადავიდეთ, ანუ ”ჩამოვიდეთ” კედლიდან: ჩვენ ვხედავთ u სიჩქარით მოძრავ კედელსა და ბურთს, რომელიც მას v + u სიჩქარით შორდება. მთლიანობაში კი ბურთი v + 2u სიჩქარით დაგვშორდება. მოძრავ კედელთან შეჯახებით ბურთმა დამატებითი აჩქარება მიიღო. არც არის გასაკვირი, ამას ხშირად ვხედავთ: ფეხბურთში (კედელი – ფეხბურთელის ფეხი), ჩოგბურთში (კედელი – ჩოგანი)…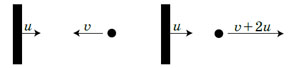

 თუ პერპენდიკულარულად არა, არამედ კუთხით დაეჯახა კედელს, მოგება სიჩქარეში მაინც იქნება, ოღონდ ცოტა. თუ საპირისპიროდ მოძრავ კედელს დაეჯახა, ბურთი მუხრუჭდება, როგორც ფეხბურთელი აჩერებს ხოლმე ფეხით მას.

 იგივე პრინციპი მოქმედებს გრავიტაციული მანევრისას – პლანეტის შემოფრენა სიჩქარის მოსამატებლად (ან პირიქით).

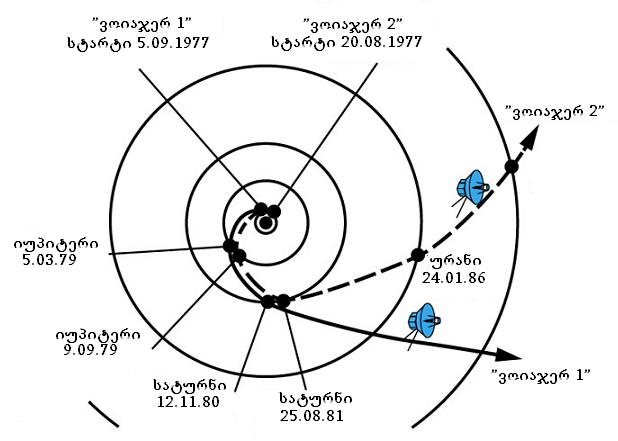
”ვოიაჯერ-1” და ”ვოიაჯერ-2”-ის ტრაექტორია.

 პლანეტა, რა თქმა უნდა, კედელი არ არის, აპარატი მას არ შეეჯახება, თუმცა ყველაფერი იგივენაირად გამოიყურება: პლანეტის მაცხოვრებლებს მოეჩვენებათ, რომ მათი პლანეტის შემოფრენის მერე, კოსმოსური აპარატი იგივე სიჩქარით შორდება მათ, როგორითაც მოფრინდა; ჩვენ კი დავინახავდით, რომ მზის გარშემო პლანეტის მოძრაობის გამო, აპარატის სიჩქარე გაიზარდა – აპარატი იმ სხვა პლანეტამ ააჩქარა.

 მაგალითდ, ავიღოთ ლეგენდარული ”კასინი”. რაკეტისგან მინიჭებული სიჩქარე (”თავისი”) მას, იუპიტერამდე მისასვლელადაც არ ეყოფოდა. ამის გამო, ის ორჯერ მიფრინდა ვენერასთან (შუალედში, ისევ დედამიწასთან), რათა აჩქარებულიყო და იუპიტერამდე მიეღწია, იქედან კი – სატურნამდე. რატომ ვენერა და არა მარსი – ეს უკანასკნელი ხომ ”გზად” უნდა შეხვდეს? იმიტომ, რომ ვენერა მეტი სიჩქარით მოძრაობს – რაც უფრო ახლოსაა პლანეტა მზესთან, მით უფრო სწრაფად მოძრაობს ის. ანუ, ვენერას საშუალებით დიდი აჩქარების აკრებაა შესაძლებელი. მაშინ, იუპიტერთან რაღა გვინდა? – სატურნამდე ნახევარ გზაზეა და იმიტომ. იუპიტერთან მისვლისას აპარატის სიჩქარე საკმაოდ შემცირდება (13 კმ/წმ), ამიტომ მცირე იუპიტერისეულ ბიძგსაც კი დიდი მნიშვნელობა ექნება. ამასთან ერთდ, მზის სისტემის ყველაზე მასიურ პლანეტის საშუალებით, აპარატის ნებისმიერი საჭირო მიმართულებით გადახრა შეგვეძლება. ”გაწრიპული” მარსისგან სარგებელი რომ მიიღოს, აპარატი ძალიან ახლოს მიდის მასთან. არანეკლებ ლეგენდარული ”როზეტა”, კომეტის (ორი კომეტის ამბორი) ორბიტაზე რომ გასულიყო, ლამის შეეხო ატმოსფეროს, ისე ახლოს ჩაუფრინა მარსს.

 კოცობრიობის მიერ კოსმოსის ათვისების ისტორიაში, კოსმოსური აპარატები 5-ჯერ გაშორდა სატურნის ორბიტას – ”პიონერები-10, 12”, ”ვოიაჯერები-1, 2”, ”ახალი ჰორიზონტები”(”ახალი ჰორიზონტები” და მზის სისტემა). ”პიონერებთან” კავშირი დაიკარგა, ხოლო 40 წლის წინათ(!) გაშვებული ”ვოიაჯერები” ახლაც აგრძელებენ მისიას. ”ვოიაჯერ-1” მზის სისტემიდან გავიდა(12.09.13(კოსმოსური სხივები და „ვოიაჯერ-1“)), ახლა 135 ასტრონომიული ერთეულით(20 მლრდ.კმ.) არის დაშორებული მზეს და 17 კმ/წმ. სიჩქარით შორდება მას(მესამე კოსმოსური სიჩქარე).

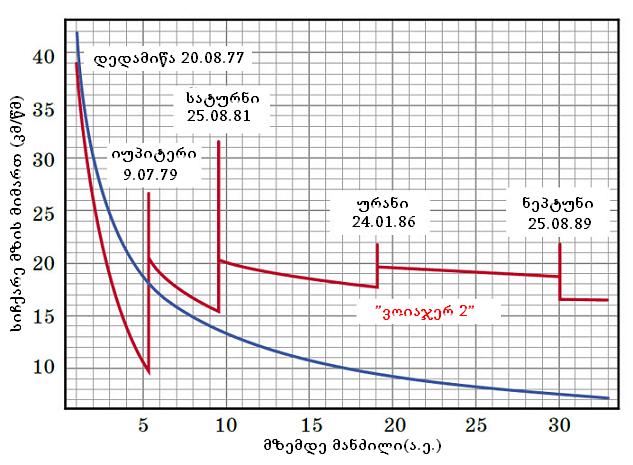
 ”ვოიაჯერ-2”-ის სიჩქარის ცვლილება მზიდან დაშორებასთან ერთდ(წითელი ხაზი); მკვეთრი მატება, პლანეტებთან გაკეთებულ გრავიტაციულ მანევრს გვიჩვენებს. ცისფრად ნაჩვენებია სიჩქარე, რომელიც ამ კონკრეტული ადგილიდან, მზის მიზიდულობის დასაძლევად არის საჭირო; იუპიტერის გარეშე ”ვოიაჯერს” სიჩქარე არ ეყოფოდა და ისევ მზისკენ დაბრუნდებოდა.

 სატურნამდე საფრენი დრო, კოსმოსური აპარატებისთვის 3-დან 8 წლამდე მერყეობს, ასე რომ 4 წელი, ნამდვილად არ არის ბევრი.

 ჯერჯერობით, ასეთ შორეულ მანძილზე ადამაიანების გადაყვანა ძალიან საშიში, ხანგრძლივი და ძვირი საქმეა: ადამიანს ხომ მეტი ადგილი სჭირდება, კოსმოსური სხივებისგან საიმედო დაცვა, ჰაერი, საჭმელი, სითბო… ასეთი ექსპედიციებისთვის ხომ ყველაფერი გრამებშია გათვლილი. ზოგიერთ აპარტს კი ნორმალურად სამუშაოდ სიცივე და სიბნელე ესაჭიროება. ადამიანი მხოლოდ ხელს თუ შეუშლიდა მათ. მოწყობილობისთვის დავალებების მიცემა, მათგან მონაცემთა აღება და დისტანციური შეკეთებაც კი, რადიოკავშირითაც შეგვიძლია.