სამყაროს შემადგენელი მატერიის სულ უფრო და უფრო მცირე ნაწილებად დაყოფით, ფუნდამენტურ და განუყოფელ ნაწილაკებს მივადგებით. ყველა მაკროსკოპული ობიექტი შეიძლება დაიყოს მოლეკულებად, ატომებად, ელექტრონებად (არ იყოფა), ბირთვად – პროტონებად და ნეიტრონებად, ბოლოს, მათში არსებულ კვარკებად და გლიუონებად. ელექტრონები, კვარკები და გლიუონები, ფუნდამენტური ნაწილაკების მაგალითია, რომელთა კიდევ უფრო მცირე ნაწილებად დაყოფა შეუძლებელია (ალბათთ). რატომ აქვს დროსა და სივრცეს ასეთი შეზღუდვები? რატომ არსებობს პლანკის სიდიდეები, რომელთა კიდევ უფრო დაქუცმაცება შეუძლებელია?
პლანკის სიდიდეებში რომ გავერკვეთ, რეალობის მმართველ ფარდობითობის ზოგად თეორიასა და კვანტურ ფიზიკას უნდა მივმართოთ.
ფარდობითობის ზოგადი თეორია, სამყაროში არსებულ მატერიასა და ენერგიას, დრო-სივრცის ქსოვილის სიმრუდესა და დეფორმაციასთან აკავშირებს. კვანტური ფიზიკა აღწერს, როგორ ურთიერთქმედებენ ერთმანეთთან სხვადასახვა ნაწილაკები ამ დრო-სივრცის შიგნით, მათ შორის ძალიან მცირე მასშტაბებზეც. არსებობს ორი ფუნდამენტური ფიზიკური კონსტანტა, ფარდობითობის ზოგადი თეორიის მთავარი ფიგურანტები: G – გრავიტაციული მუდმივა, და c – სინათლის სიჩქარე. G , ნივთიერება-ენერგიით გამოწვეული დრო-სივრცის დეფორმაციის მაჩვენებელს გვკარნახობს. c კი ამ დეფორმაციების გავრცელების(ურთიერთქმედების) სიჩქარეს.
ფუნდამენტური კონსტანტები გვაქვს კვანტურ მექანიკაშიც: c და h, ეს უკანასკნელი – პლანკის მუდმივაა (პლანკის მუდმივა). c – ყველა ნაწილაკის სიჩქარის შეზღუდვაა, სიჩქარე, რომლითაც ყველა უმასო ნაწილაკმა უნდა იმოძრაოს, ურთიერთქმედების გავრცელების მაქსიმალური სიჩქარე. პლანკის მუდმივა უმნიშვნელოვანესია კვანტური ენერგეტიკული დონეების დაკვანტვის, ნაწილეკაბს შორის ურთიერთქმედებისა და მოვლენათა ყველა შესაძლებელი შედეგების აღწერისთვის. პროტონის გარშემო მბრუნავ ელექტრონს, სხვადასხვა ენერგეტიკული დონე შეიძლება ჰქონდეს, რომლებიც დისკრეტული ნაბიჯებით იცვლება, ეს ბიჯი კი h-ით განისაზღვრება.
სიგრძის, მასისა და დროის სკალის შესაქმნელად, ამ სამი მუდმივას კომბინაციებით სარგებლობა შეგვიძლია. მათი მნიშვნელობები ცნობილია, შესაბამისად, პლანკისეული სიგრძეც, პლანკისეული მასაც და პლანკისეული დროც (შეგვიძლია გავიგოთ პლანკის ენერგია, ტემპერატურა და ა.შ.) (აქვს თუ არა ტემპერატურას ზღვარი?).
წარმოიდგინეთ, რომ გვაქვს რაღაც გარკვეული მასის ნაწილაკი. შეიძლება გაგვიჩნდეს შეკითხვა:”ამ ნაწილაკის მასის შეუცვლელად, რამდენად მცირე მოცულობამდე უნდა შევამციროთ იგი, რომ შავ ხვრელად გადაიქცეს? ან: შავი ხვრელი რომ მქონდეს, სინათლის სიჩქარით მოძრავი ნაწილაკი რამდენ ხანში გაივლიდა ამ ხვრელის ზომის მანძილს?”. პლანკისეული მასა, სიგრძე და დრო, სწორედ ასეთ სიდიდეებს შეესაბამება: პლანკისეული ზომის შავი ხვრელს ექნება პლანკისეული სიგრძე და მისი გავლა სინათლის სხივის სიჩქარით იქნება შესაძლებელი პლანკისეულ დროში.
პლანკის მასა, ნებისმიერი ნაწილაკის მასაზე გაცილებით მეტია. პროტონის მასაზე (ატომი) 1019-ჯერ მეტი! პლანკის სიგრძე, ნებისმიერ ჩვენს მიერ გაზომილზე 1014-ჯერ მცირეა, ხოლო ნებისმიერ ჩვენს მიერ პირდაპირ გაზომილ დროზე 1025-ჯერ მცირე (იოქტოწამი(y)). ჩვენთვის ეს მასშტაბები ხელმიუწვდომელია, თუმცა ძალიან მნიშვნელოვანი: პლანკის ენერგია (რომლის მიღება პლანკის მასის E = mc2 ფორმულაში ჩასმით შეიძლება) – არის მასშტაბი, რომელზეც კვანტურ-გრავიტაციული ეფექტები ვლინდება.
ეს იმას ნიშანავს, რომ პლანკისეულ ენერგიაზე, ან პლანკის დროზე მცირე მონაკვეთში, ან პლანკის სიგრძეზე მცირე დისტანციაზე, ჩვენთვის ცნობილი ფიზიკის კანონები უნდა დაირღვეს. საქმეში, კვანტური გრავიტაციის ეფექტები ერთვება, ხოლო ფარდობითობის ზოგადი თეორია ისეთი საიმედო ვეღარ არის. სივრცის სიმრუდე ძალიან დიდი ხდება, ხოლო ”ფონი”, რომელსაც კვანტური სიდიდეების გამოთვლისთვის ვიყენებთ, ასევე არასაიმედო. ენერგიისა და დროის განუსაზღვრელობა იმას ნიშნავს, რომ განუსაზღვრელობები იმ მნიშვნელობებზე მეტი ხდება, რომელთა გაზომვაც ვიცით. მოკლედ რომ ვთქვათ, ჩვენთვის ჩვეული ფიზიკის კანონები ვეღარ გამოგვადგება.
სამყაროსთვის ეს პრობლემას არ წარმოადგენს. ეს ენერგეტიკული მასშტაბი 1015-ჯერ მეტია იმაზე, რომლის მიღწევა დიდ ადრონულ კოლაიდერს შეუძლია და 100 000 000-ჯერ მეტი იმ ყველაზე მაღალი ენერგიის მქონე ნაწილაკების ენერგიაზე, რომელთაც თვითონ სამყარო ქმნის (რეკორდსმენი სხივები; თქვენი სმარტფონი ყველაზე დიდი ტელესკოპის ნაწილი გახდება…). 10 000-ჯერ მეტი მაჩვენებლებზე, რომლებსაც სამყარომ დიდი აფეთქების მომენტში მიაღწია. შავი ხვრელების ცენტრში არსებული სინგულარობის შესწავლა თუ გვინდა, სწორედ ამ ზღვრულ მნიშვნელობებთან გვექნება საქმე. ამ ადგილებში თავმოყრილი მასა (პლანკისაზე გაცილებით მეტი) შეკუმშულია ზომამდე, რომელიც თეორიულად პლანკის სიგრძეზე მცირეა. დღეისათვის ის ჩვენთვის მიუწვდომელია, რადგან შავი ხვრელის მოვლენათა ჰორიზონტით არის ჩაკეტილი (შავი ხვრელების საიდუმლო).
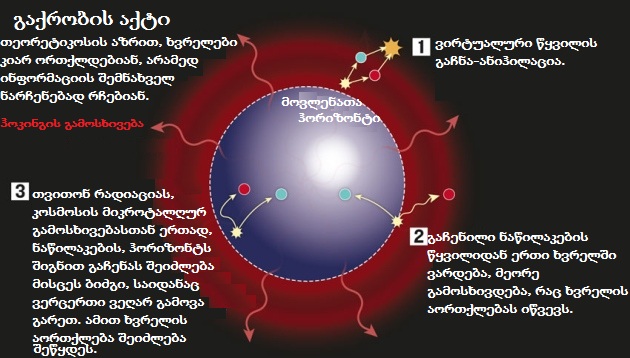
შავი ხვრელებიც იშლება. ველის კვანტური თეორიის ინტეგრაცია ფარდობითობის ზოგადი თეორიის გამრუდებულ დრო-სივრცესთან, გვიჩვენებს, რომ მოვლენათა ჰორიზონტს გარეთ მცირე გამოსხივება ჩნდება, რომლის ენერგიაც ხვრელის მასიდან ამოდის. დროთა განმავლობაში შავი ხვრელის მასა მცირდება, მოვლენათა ჰორიზონტი იკუმშება, მზის მასის მქონე შავი ხვრელი 1067 წლის მერე მთლიანად ორთქლდება. ხვრელის სრულ გამოსხივებასთან წვდომა რომ შეგვძლებოდა, მისი არსებობის ბოლო მომენტების ჩათვლით, ყველა იმ მკვანტური ეფექტების ერთად თავმოყრას შევძლებდით, რომელთა წინასწარმეტყველება ყველაზე უფრო საუკეთესო თეორიებითაც კი ვერ ხერხდება (შავი ხვრელის სიცოცხლის ხანგრძლივობა).
არ არის აუცილებელი, რომ სივრცის კიდევ უფრო მცირე ნაწილებად დაყოფა შეგვეძლოს, ვიდრე პლანკის ზომაა, ან დროის დაყოფა პლანკის დროზე ნაკლებ ინტერვალებად. უბრალოდ ვიცით, რომ სამყაროს ჩვენეული აღქმა, ფიზიკის კანონები, ამ მასშტაბებს ვერ გაცილდება. დრო იკვანტება? მართლა უწყვეტად მიედინება თუ არა? რა ვუყოთ იმ ფაქტს, რომ ჩვენთვის ცნობილ ფუნდამენტურ ნაწილაკებს, პლანკის მასაზე გაცილებით ნაკლები მასა გააჩნიათ? ეს შეკითხვები ისევ პასუხგაუცემელი რჩება. პლანკისეული მასშტაბებით ჩვენი წარმოდგენებია შეზღუდული, არა თვითონ სამყარო. ექსპერიმენტირებას ვაგრძელებთ. რაც უფრო მეტი ცოდნა გვექნება, მით მეტ შეკითხვაზე შევძლებთ პასუხის გაცემას (რაც უფრო ზუსტია საათი, მით უფრო ბუნდოვანი ხდება დრო).
