შავი ხვრელის მოვლენათა ჰორიოზონტს შიგნით მოხვედრის მერე, უკან ვეღარაფერი გამოვა. არ არსებობს სიჩქარე, თუნდაც სინათლის, რომლითაც ხვრელის გრავიტაცია დაიძლევა. ფარდობითობის ზოგადი თეორიის მიხედვით, სივრცე, მასამ და ენერგიამ შეიძლება გაამრუდოს, ხოლო შავი ხვრელების შერწყმა ასეთი გამრუდების ყველაზე უფრო ექსტრემალური ვარიანტია.
თუ არის შესაძლებელი ხვრელის მოვლენათა ჰორიზონტის გადაკვეთა და უკან გამოსვლა, როცა მოვლენათა ჰორიზონტის დეფორმირებას მასიური შერწყმა ახდენს? ერთი ხვრელის ჰორიზონტიდან მეორეში გაქცევა? ორივეს ჰორიზონტიდან გამოსვლა?

ჩვეულებრივ, შავი ხვრელი მასიური ვარსკვლავის ბირთვის კოლაფისთ(შეკუმშვა) ჩნდება, ან ზეახლად აფეთქებით ან ნეიტრონული ვარსკვლავების შერწყმის მერე, ან პირდაპირი კოლაფსით.

თვითონ შავ ხვრელს, ასე რომ ვთქვათ, არ ”ახსოვს”, რა ნაწილაკები ჩავარდა მასში, რა კვანტური მდგომარეობებით. ინფორმაციული თვალსაზრისით, რაც რჩება – შავი ხვრელის საერთო მასა, მუხტი და კუთხური მომენტია(რაც შავი ხვრელების შესახებ უნდა ვიცოდეთ).
შეიძლება წარმოვიდგინოთ სცენარი, რომლის მიხედვითაც მატერია შავ ხვრელში ხვდება, ზუსტად იმ მომენტში, როცა ერთი ხვრელი მეორეს უნდა შეუერთდეს. აკრეციული დისკო ყველა ხვრელს აქვს, რომელშიც ვარსკვლავთშორისი მატერია ბრუნავს, საიდანაც ნაწილაკები მოვლენათა ჰორიზონტს მუდმივად კვეთენ. წარმოვიდგინოთ ნაწილაკი, რომელიც შავ ხვრელში, მეორე ხვრელთან შერწყმის ფინალურ ეტაპამდე მოხვდა.
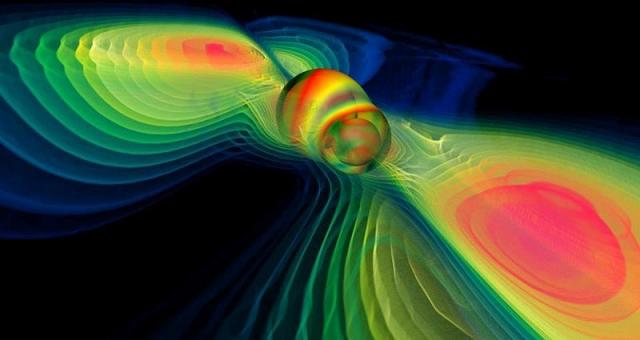
შავი ხვრელების შერწყმა, მათი ერთმანეთის გარშემო ძალიან ხანგრძლივი სპირალური მოძრაობის მერე ხდება, ენერგიის გამოსხივებით გრავიტაციული ტალღების სახით. ენერგია ფინალურ მომენტამდე სხივდება და სივრცეში ვრცელდება. ამით მოვლენათა ჰორიზონტის ან თვითონ შავი ხვრელის შეკუმშვა ვერ მოხდება. ენერგია, საერთო მასათა სივრცე-დროდან ამოდის, რომელიც სულ უფრო და უფრო ძლიერად დეფორმირედება. ასეთნაირად, პლანეტა მერკურისაც შეიძლება მოპარო ენერგია, თუმცა ის(და მზე) თვისებებს არ შეიცვლის.
შერწყმის ბოლო მომენტის დადგომისას, ორი შავი ხვრელის მოვლენათა ჰორიზონტებს ერთმანეთის გრავიტაციული ზემოქმედება ადეფორმირებს. რელატივისტებმა უკვე გამოთვალეს, როგორ ზემოქმედებს შერწყმა მოვლენათა ჰორიზონტებზე, რაც შთამბეჭდავად ინფორმატიულია.
მიუხედავად იმისა, რომ შერწყმამდე შავი ხვრელების საერთო მასის 5% გრავიტაციული ტაღების სახით შეიძლება გამოსხივდეს, მოვლენათა ჰორიზონტი მაინც არ პატარავდება. მნიშვნელოვანია, რომ თანაბარი მასის ორი შავი ხვრელის ჰორიზონტები სივრცის გარეკვეულ მოცულობას იკავებს. თუ მათ გაორმაგებული მასის ხვრელის სახეს მივცემთ, ჰორიზონტის მიერ დაკავებული სივრცის მოცულობა, გაერთიანებული ხვრელების საწყის მოცულობაზე ოთხჯერ მეტი იქნება. შავი ხვრელების მასა მათი რედიუსების პირდაპირ პროპორციულია, ხოლო მოცულობა – რადიუსის კუბის.
აღმოჩნდა, რომ რაც არ უნდა უძრავად გავაჩეროთ ნაწილაკი მოვლენათა ჰორიზონტს შიგნით, სინგულარობისკენ მაქსიმალურად ნელი ვარდნით, იქედან უკან ამოსვლის არანაირი შანსი არ ექნება. შეთავსებული მოვლენათა ჰორიზონტების საერთო მოცულობა შერწყმისას გაიზრდება და ნაწილაკის მოძრაობის ტრაექტორიის მიუხედავად, ის ორივე ხვრელის გაერთიანებულ სინგულარობაში ვარდნისთვის იქნება განწირული(უცნაური სინგულარობა).
მოდელირებულ პროცესებში ამოფრქვევებიც ჩნდება, როცა კატაკლიზმის დროს მატერია გაქცევას ახერხებს, ხოლო რაც ხვრელებს შიგნით იყო, შიგნითვე რჩება; გარეთ არსებული მატერიის მეტი ნაწილი ხვრელში შთაინთქმება, მხოლოდ მცირედი ახერხებს გაქცევას. ხვრელში მოხვედრილი მატერია მუდმივად იქ დარჩება, მეორეს(ხვრელის) შემოჭრა ძალთა ბალანსს ვერ შეცვლის.
