სივრცეში ენერგიის გადაცემა ნაწილაკების ან ტალღების საშუალებით ხდება. მაგალითისთვის, წარმოვიდგინოთ მაგიდის ნაპირზე დადებული დომინოს ქვა, მაგიდიდან მისი გადაგდება ორი ხერხითაა შესაძლებელი.
ვესროლოთ სხვა ქვა (ანუ გადავცეთ წერტილოვანი იმპულსი ნაწილაკის საშუალებით), ან მასთან ახლოს დავაწყოთ დანარჩენი ქვების წყობა და პირველი ქვა მეორეს დავაჯახოთ. მეორე, მესამეს დაეჯახება, მესამე, მეოთხეს და ა.შ, სანამ ბოლო ქვა ნაპირზე მდგომს გადააგდებს მაგიდიდან, ანუ ენერგია ტალღის სახით გადავეცით მას. ყოველდღიურ ცხოვრებაში ენერგიის გადაცემის ამ ორ მექანიზმში წინააღმდეგობები არ დაიმზირება. მაგალითად, კალათბურთის ბურთი ნაწილაკია, ხოლო ხმა ტალღა, მორჩა და დამთავრდა.
 კვანტურ მექანიკაში კი ყველაფერი ისე არ ხდება, როგორც მაკროსამყაროში. სინათლე, რომელიც ჩვენს წარმოდგენაში ტალღაა, ისე იქცევა, თითქოს ნაწილაკების (ფოტონების) ნაკადი იყოს, ხოლო ელემენტარული ნაწილაკები, როგორიცაა ელექტრონი და მასიური პროტონიც კი, ტალღურ თვისებებს ავლენს.
კვანტურ მექანიკაში კი ყველაფერი ისე არ ხდება, როგორც მაკროსამყაროში. სინათლე, რომელიც ჩვენს წარმოდგენაში ტალღაა, ისე იქცევა, თითქოს ნაწილაკების (ფოტონების) ნაკადი იყოს, ხოლო ელემენტარული ნაწილაკები, როგორიცაა ელექტრონი და მასიური პროტონიც კი, ტალღურ თვისებებს ავლენს.
ახლა კი ზემოთ თქმულის საილუსტრაციო მარტივი ექსპერიმენტი ჩავატაროთ. დავუშვათ, რომ გვაქვს დახურული კამერა ვერტიკალური ორი თხელი ჭრილით, რომლებისკენაც პარალელური სინათლის კონებია მიმართული. შეიძლება ვიფიქროთ, რომ სინათლის შემადგენელი ნაწილაკები ჭრილებს გაივლიან და კამერის უკანა კედელზე (ეკრანზე) ორი მკაფიო ჭრილის ფორმის განთებული ხაზები გამოჩნდება, რომელთა შორისაც შუქი არ უნდა მოხვდეს.
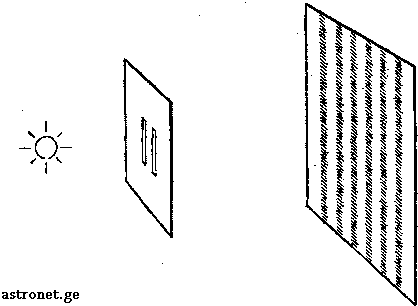 პრაქტიკაზე კი ჩვენ სრულიად განსხვავებულ სურათს ვხედავთ. ჰიუიგენსის პრინციპის მიხედვით, თითოეული ჭრილი მეორადი სინათლის დამოუკიდებელი წყაროს როლს თამაშობს, ამიტომ ეკრანზე, ორ ჭრილს შორის, მათი რხევების ამპლიტუდის მაქსიმუმი უნდა დავინახოთ. კერძოდ, ხმის ტალღები, რომლებიც ორი სტერეოდინამიკიდან გამოდის, ხმის სიმაღლის პიკს სწორედ მათგან ერთნაირად დაშორებულ ხაზზე იძლევა. ასევე ხდება ერთნაირი მანძილით დაშორებული სინათლის წყაროების შემთხვევაშიც, რომლებიც ეკრანზეა პროექცირებული. სხვა სიტყვებით რომ ვთქვათ, ტალღების ამპლიტუდის პიკი იმ სივრცულ ზონაზე მოდის, სადაც, კორპუსკულარული თეორიის მიხედვით, ნაწილაკთა მინიმალური რაოდენობა უნდა მოხვდეს.
პრაქტიკაზე კი ჩვენ სრულიად განსხვავებულ სურათს ვხედავთ. ჰიუიგენსის პრინციპის მიხედვით, თითოეული ჭრილი მეორადი სინათლის დამოუკიდებელი წყაროს როლს თამაშობს, ამიტომ ეკრანზე, ორ ჭრილს შორის, მათი რხევების ამპლიტუდის მაქსიმუმი უნდა დავინახოთ. კერძოდ, ხმის ტალღები, რომლებიც ორი სტერეოდინამიკიდან გამოდის, ხმის სიმაღლის პიკს სწორედ მათგან ერთნაირად დაშორებულ ხაზზე იძლევა. ასევე ხდება ერთნაირი მანძილით დაშორებული სინათლის წყაროების შემთხვევაშიც, რომლებიც ეკრანზეა პროექცირებული. სხვა სიტყვებით რომ ვთქვათ, ტალღების ამპლიტუდის პიკი იმ სივრცულ ზონაზე მოდის, სადაც, კორპუსკულარული თეორიის მიხედვით, ნაწილაკთა მინიმალური რაოდენობა უნდა მოხვდეს.
 თუ ასეთი კამერისკენ ელექტრონების კონას მივმართავთ, ეკრანზე, ტალღებისთვის დამახასიათებელი, გამოსხივების ინტენსიურობის პიკებისა და ვარდნების ზოლები გამოჩნდება, ანუ ელექტრონი იქცევა როგორც ტალღა. მეორეს მხრივ, თუ ელექტრონებს თითო-თითოდ ”გავისვრით”, ყოველი მათგანი ეკრანზე მკაფიო კვალს დატოვებს – ანუ მოიქცევა როგორც ნაწილაკი. ფოტონების შემთხვევაშიც იგივე ხდება – მათი ნაკადი ტალღის თვისებებს ავლენს, ხოლო ცალკეული ფოტონი – ნაწილაკის. მიკროსამყაროს ობიექტები, რომლებიც ნაწილაკურ ბუნებას ავლენენ, თითქოს ისიც სულ ”ახსოვთ”, რომ მათ ტალღური ბუნებაც გააჩნიათ და პირიქით. მიკროსამყაროს ობიექტთა ამ უცნაურ თვისებას კვანტურ-ტალღური დუალიზმი ეწოდება.
თუ ასეთი კამერისკენ ელექტრონების კონას მივმართავთ, ეკრანზე, ტალღებისთვის დამახასიათებელი, გამოსხივების ინტენსიურობის პიკებისა და ვარდნების ზოლები გამოჩნდება, ანუ ელექტრონი იქცევა როგორც ტალღა. მეორეს მხრივ, თუ ელექტრონებს თითო-თითოდ ”გავისვრით”, ყოველი მათგანი ეკრანზე მკაფიო კვალს დატოვებს – ანუ მოიქცევა როგორც ნაწილაკი. ფოტონების შემთხვევაშიც იგივე ხდება – მათი ნაკადი ტალღის თვისებებს ავლენს, ხოლო ცალკეული ფოტონი – ნაწილაკის. მიკროსამყაროს ობიექტები, რომლებიც ნაწილაკურ ბუნებას ავლენენ, თითქოს ისიც სულ ”ახსოვთ”, რომ მათ ტალღური ბუნებაც გააჩნიათ და პირიქით. მიკროსამყაროს ობიექტთა ამ უცნაურ თვისებას კვანტურ-ტალღური დუალიზმი ეწოდება.
კომპლემენტარობის პრინციპი, ამ ფაქტის მარტივი კონსტატაციაა. პრინციპის მიხედვით, კვანტური ობიექტი შეგვიძლია წარმოვადგინოთ ნაწილაკის ან ტალღის სახით და ეს წარმოდგენები არ ეწინააღმდეგება ერთმანეთს, ისინი ერთმანეთს ავსებს, რაზეც თვითონ პრინციპის სახელიც მეტყველებს.
აშკარაა, რომ მიკროსამყაროს ობიექტების ქცევა პრინციპულად განსხვავდება ჩვენთვის ჩვეული მაკროსამყაროს ობიექტების ქცევისაგან. მაგრამ რატომ? სინამდვილეში, ელექტრონები და ფოტონები არც ნაწილაკებია და არც ტალღები, არამედ სრულიად განსხვავებული რამ თავიანთი შინაგანი ბუნებით, რის გამოც არ ემორჩილებიან ჩვენი ყოველდღიური ცხოვრებისთვის ჩვეული ტერმინებით აღწერას. თუ კიდევ უფრო ვეცდებით ჩვენთვის ნაცნობი პარადიგმების ჩარჩოებში მათ მოქცევას, კიდევ უფრო მეტ პარადოქსებს წავაწყდებით. ასე რომ, მთავარი დასკვნა შემდეგშია – ჩვენს მიერ დამზერადი დუალიზმი არა კვანტური ობიექტებისთვის თანდაყოლილი თვისებებითაა გაჩენილი, არამედ კატეგორიების არასრულფასოვნებით, რომლებითაც ჩვენ ვაზროვნებთ 🤔
2025 წელს, ნილს ბორის დაბადებიდან 140 წელი შესრულდება. ის იყო არა მხოლოდ გამოჩენილი ფიზიკოსი, კვანტური თეორიის ერთ-ერთი შემქმნელი, არამედ მოაზროვნეც, რომლის წვლილიც ფილოსოფიაში, მისი კოლეგის, ვერნერ ჰაიზენბერგის თქმით, აღემატება მის მიღწევებს ფიზიკაში, რომლებმაც 1922 წელს, ნობელის პრემია მიიღო. ბორი, რომელმაც მნიშვნელოვანი როლი ითამაშა ფიზიკის ფილოსოფიური საფუძვლების გადახედვაში (რაც აუცილებელი იყო კვანტური ფენომენების გასაგებად), საკუთარ თავს ფილოსოფოსად არ თვლიდა. უნდა ითქვას, რომ მისი შემოქმედების ეს ასპექტი ნაკლებად ცნობილია (ფილოსოფიური ნაშრომების სამტომეული მხოლოდ 1987 წელს, მისი გარდაცვალებიდან 25 წლის შემდეგ გამოიცა), თუმცა ის არანაკლებ მნიშვნელოვანი და საინტერესოა, ვიდრე მისი მიღწევები ფიზიკასა და სოციალურ საქმიანობაში.

ერთი და იგივე მოვლენაზე სხვადასხვა ინსტრუმენტებით დამზერისას მიღებული აღწერილობა, ურთიერთგამომრიცხავი აღმოჩნდება ხოლმე, რის გამოც ბორმა, დამატებითობის კონცეფცია უწოდა ამას. დამატებითობის მაგალითები არა მხოლოდ კვანტურ ფიზიკაში გვხვდება. ისინი ყველგან გვაკრავს გარს: გრძნობა–გონება, სერიოზულობა–იუმორი და ა.შ. ბორის ეს პრინციპი გვასწავლის, რომ თავი ავარიდოთ ერთ მიდგომას სხვადასხვა თვისებების განხილვისას, რომელთა გამოვლინება მხოლოდ ურთიერთგამომრიცხავ პირობებში შეიძლება მოხდეს. შესაძლოა, ამ ტიპის საკითხებში მრავალი სირთულის გადაჭრის საუკეთესო გზა არის საერთოდ არ იფიქრო მათზე, რასაც აინშტაინი „ბორ-ჰაიზენბერგის დამამშვიდებელ ფილოსოფიას“ უწოდებდა. ამავდროულად, ბორი თვლიდა, რომ დამატებითობის გამოყენებით შესაძლებელია რეალობის უფრო ღრმა გაგების მიღწევა.
ჩინეთის მეცნიერებისა და ტექნოლოგიების უნივერსიტეტის მკვლევრებმა, ანჰუის პროვინციის დედაქალაქ ჰეფეიშიდან, და მათმა კოლეგებმა, შანხაის კვანტური კვლევების ცენტრიდან, ძალიან ელეგანტური და უაღრესად ზუსტი ექსპერიმენტი ჩაატარეს, კვანტური მექანიკის ორი ქვაკუთხედის: განუსაზღვრელობის პრინციპისა და კომპლემენტარობის პრინციპის შესამოწმებლად. ბორის არგუმენტები, თეორიულად ძალიან დამაჯერებელი იყო. ამავდროულად, ბოლო ათწლეულების განმავლობაში არაერთი მცდელობის მიუხედავად, ისინი არასდროს ყოფილა ექსპერიმენტულად სანდოდ დადასტურებული. სწორედ ამას მიაღწიეს ჩინელმა ფიზიკოსებმა ახლა.
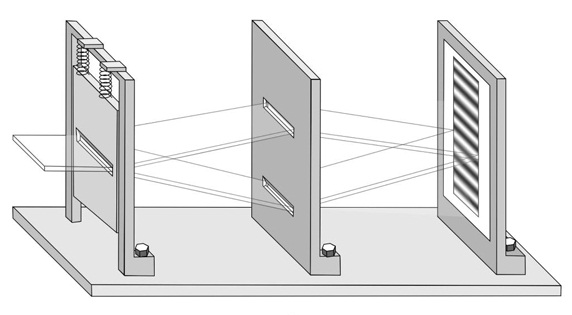
რა თქმა უნდა, მათ რაიმე ულტრამგრძნობიარე მექანიკური მოწყობილობა არ შეუქმნიათ, როგორც აინშტაინის წარმოსახვით ექსპერიმენტში შემოთავაზებული ზემგრძნობიარე ზამბარები, რომლებიც ზემოთ ხსენებული ორჭრილიანი დაფის წინ, ერთჭრილიან დაფას ამოძრავებდა, ზემოთ და ქვემოთ მოძრავ ფოტონებს დაიჭერდა, რაც ინტერფენციული სურათის გაქრობას გამოიწვევდა. ამის ნაცვლად, მათ გამოიყენეს რუბიდიუმ-87-ის ერთი ატომი, რომელიც სამგანზომილებიან ოპტიკურ ხაფანგში იყო გამომწყვდეული და აბსოლუტურ ნულთან ახლო ტემპერატურამდე მიყვანილი. ხაფანგის შესაქმნელად გამოყენებული იქნა 852 ნმ. ტალღის სიგრძის ინფრაწითელი ლაზერი. ამ პირობებში, დაჭერილი ატომის იმპულსის კვანტური გაურკვევლობა შედარებადი იყო ფოტონების იმპულსთან, რომელბითაც ამ ატომს ასახივებდნენ. სწორედ ასე გახდა შესაძლებელი მისი გამოყენება აინშტაინის წარმოსახვით ექსპერიმენტში, მოძრავი ერთჭრილიანი ეკრანის კვანტურ ანალოგად.
ამ ექსპერიმენტის ტექნიკური დეტალები საკმაოდ რთულია, მაგრამ მისი ზოგადი სქემა მარტივად აიხსნება – რა თქმა უნდა, გარდაუვალი გამარტივებებით. ხაფანგის სიღრმე შეიძლება შეიცვალოს, რაც ატომს მოძრაობის მეტ-ნაკლებ თავისუფლებას ანიჭებს. პირველ შემთხვევაში, მისი პოზიცია შეიძლება მნიშვნელოვნად შეიცვალოს თითოეული ფოტონის ზემოქმედებისას; მეორეში, ის პრაქტიკულად უძრავად რჩება. კვანტური მექანიკის პრინციპების თანახმად, რასაც შეიძლება მოველოდეთ ძლიერად დაბლოკილი ატომისგან არის, რომ ის პრაქტიკულად რეაგირებას არ მოახდენს ფოტონების შეჯახებაზე და ინტერფენერნიცის უნარს შეინარჩუნებენ. სუსტადბლოკირებული ატომი, პირიქით, ფოტონებით ბომბარდირებას “შეამჩნევს” და მათი მოძრაობის შესახებ ინფორმაციას მოგვაწვდის. ამ შემტხვევაში ფოტონური ინტენფერენცია გადღაბნილი აღმოჩნდება.
სწორედ ეს გვიჩვენა ჩინელი მეცნიერების ექსპერიმენტმა. თუ მასში საჭვო ვერაფერი აღმოაჩინეს, ფიზიკის კიდევ ერთი საუკუნიანი პრობლემა შეიძლება ჩაითვალოს გადაიჭრილად (journals.aps.org).

თუ არ ვცდები, ორი ჭრილის ექსპერიმენტში ელექტრონების თუ ფოტონების “თითო-თითოდ გასროლის” შემთხვევაშიც კი, როცა “გასროლების” რაოდენობა დიდია, ეკრანზე ინტერფერენციული სურათი ჩნდება. შესაბამისად, ცალკეული ფოტონი თუ ელექტრონიც ავლენს ტალღურ ბუნებას.
აინშტაინის ფარდობითობა დიდი სისულელეა, რადგან დრო არ არსებობს. ამ სისულელემ დაკვირვება “გაამრუდა” და ჩიხში შეიყვანა, რაც კვანტური ფიზიკის კვლევებაც წარმოაჩინა. ადამიანს ხელეწიფება ცვალოს თავისი დაკვირვების მასშტაბები და ინტენსივობა. ამიტომ დაკვირვების შედეგები შედარებითია დაკვირვების შედეგების მასშტაბისა და ინტენსივობის შესაბამისად, რასაც ბრწინვალედ აღწერს კვანტური ფიზიკა. შეუძლებელია ობიექტური სამყაროს მთლიანი სურათის დანახვა, თუ რატომ ეს კიდევ ცალკე საკითხია, თუმცა პასუხები ფილოსოფიურად ძალიან მარტივია, რომლის გამოყენებით ფორმულებში გადაყვანა კომპლექსური კვლევის საგანია და ახალ ტექნოლოგიურ ერას შექმნის, თუ წესიერად მოიქცეცვა ადამიანი.
”აინშტაინის ფარდობითობა დიდი სისულელეა”, ამას რომ ასე ადვილად ამბობთ, ე.ი.ხვალვე უნდა ველოდე თქვენ ნაშრომს ცნობილ მეცნიერულ ჟურნალებში.