ნაწილაკთა კოლექტივის განსაკუთრებულად მნიშვნელოვანი მახასიათებელია ინვარიანტული მასა, რომელიც ერთმანეთის მიმართ მათ გაფანტვას აღწერს.
სიჩქარის ზრდასთან ერთად მასა არ იზრდება!
არსებობს ფართოდ გავრცელებული აზრი, რომ მასა, სიჩქარის ზრდასთან ერთად იზრდება. მას ხშირად ”რელატივისტურ მასას” უწოდებენ. ეს ყველაფერი ენერგიასა და მასას შორის არსებული კავშირის არასწორ ინტერპერტაციას უკავშირდება: თუ სიჩქარის მატებასთან ერთად ენერგია იზრდება, მაშინ მასაც უნდა გაიზარდოს – ასეთი განსჯა არასწორია. მასა, ისეთი სახით, რომლითაც მას თანამედროვე ფიზიკა წარმოგვიდგენს, მით უმეტეს ელემენტარული ნაწილაკების ფიზიკა, სიჩქარეზე დამოკიდებული არ არის(ელემენტარული ნაწილაკების სტანდარტული მოდელი). სიჩქარეზე, ნაწილაკის ენერგია და იმპულსია დამოკიდებული, სინათლის მახლობელ სიჩქარეებზე დინამიკისა და კინემატიკის კანონები იცვლება. ნაწილაკის მასა, სიდიდე, დამოკიდებული სრულ ენერგიასა(E) და იმპულსზე(p), ფორმულირებით m2 = E2/c4 – p2/c2, უცვლელი რჩება. პოპულარულ გამოცემებში ამ სიდიდეს ”უძრაობის მასას” უწოდებენ და ”რელატივისტურ მასას” უპირისპირებენ, თუმცა, კიდევ ერთხელ ავღნიშნოთ: ასეთი დაყოფა მხოლოდ პოპულარულ მასალებსა და ფიზიკის ზოგიერთ კურსებში ხდება. თანამედროვე ფიზიკაში არანაირი ”რელატივისტური მასა” არ არსებობს, მასში მხოლოდ ”მასაა”, განსაზღვრული ამ განტოლებით. ტერმინი ”რელატივისტური მასა”, ფიზიკის პოპულარიზაციისთვის მოგონილი ცუდი ფანდია, ჭეშმარიტი ფიზიკიდან შორს მყოფი.
ინვარიანტული მასა
დავუშვათ, გვაქვს ნაწილაკები ენერგიებით E1, E2 და იმპულსებით p1 და p2(მსხვილი შრიფტი იმპულსის ვექტორულობაზე(გააჩნია მიმართულება) მიუთითებს). არა აქვს მნიშვნელობა, ეჯახებიან ეს ნაწილაკები ერთმანეთს თუ შორდებიან. მათი მასები, რა თქმა უნდა, ზემოთ მოყვანილი ფორმულით გამოითვლება.
ახლა კი დავუშვათ, რომ ამ ორი ნაწილაკის, როგორც ერთიანი სისტემის, თვისებათა გაგება გვინდა. შეგვიძლია დავწეროთ ამ სისტემის სრული ენერგია E12 და სრული იმპულსი p12, E12= E1 + E2, p12 = p1 + p2, იმპულსები ჩაიწერება როგორც ვექტორები. ანუ, რაღაც მასის მსგავსი სიდიდე m12 შეიძლება მივიღოთ ფორმულით m122 = E122/c4 – p122/c2.
სწორედ სიდიდე m12 არის ნაწილაკთა წყვილის ინვარიანტული მასა. მისი უმნიშვნელოვანესი თვისება ზუსტად ისაა, რომ ის ინვარიანტულია, არ არის დამოკიდებული ათვლის სისტემაზე, რომელშიც ჩვენ გამოთვლბს ვახდენთ(ენერგიისა და იმპულსისგან განსხვავებით).
მიაქციეთ ყურადღება, რომ ინვარიანტული მასა სულაც არ არის ორი ნაწილაკის მასათა ჯამი! უფრო მეტიც, მარტივი დასამტკიცებელია, რომ m12 ≥ m1 + m2, თან ტოლობა მხოლოდ მაშინაა შესაძლებელი, როცა ორი ნაწილაკი ერთნაირი სიჩქარით მოძრაობს(ანუ ერთი ნაწილაკი უძრავია, მეორეს მიმართ). ამრიგად, ორი ნაწილაკისთვის სამი სხვადასხვა დამოუკიდებელი მონაცემი გვაქვს, ათვლის სისტემისგან დამოუკიდებელი: m1, m2 და m12.
თუ ჩვენ ორზე მეტ ნაწილაკს ვსწავლობთ, მაშინ ინვარიანტული მასები მსგავსი წესებით არა მარტო მთლიანად სისტემის, არამედ ნებისმიერი წყვილისთვის, სამეულისთვის და საერთოდ ამ ნაწილაკთა ნებისმიერი კომბინაციისთვის შეგვიძლია გამოვითვალოთ. აღსანიშნავია, რომ ამ მასების დადგენით, ჯერ კიდევ არ შეგვიძლია მათ წარმოშობასა და ურთიერთ ზემოქმედებაზე საუბარი. ეს, უბრალოდ, დამატებითი კინემატიკური მონაცემებია, რომლებიც არ არის დამოკიდებული ათვლის სისტემაზე.
ინვარიანტული მასა, ოგორც ნაწილაკთა წარმოშობის ”ნიშანი”
ინვარიანტული მასა გვეუბნება, თუ რამდენად ბობოქარია ნაწილაკთა ურთიერთ გაფანტვა, რამდენად ინტენსიურია ეს გაფანტვა(ან შეჯახება, თუ შეჯახებაზეა საუბარი). კიდევ უფრო მარტივად რომ ვთქვათ, თუ ამ გაფანტვას ნაწილაკთა კოლექტივის ”მიკროაფეთქების” სახით წარმოვიდგენთ, მაშინ ინვარიანტული მასა ამ მიკროაფეთქების ”ენერგეტიკული ბალანსის” მახასიათებელი იქნება.
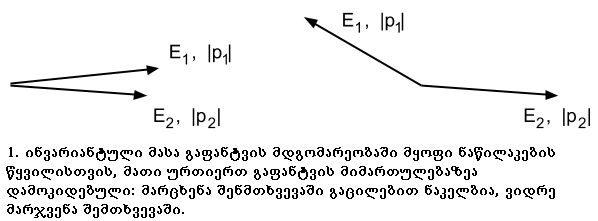
ინვარიანტული მასისგან მიღებული უმთავრესი სარგებელი ისაა, რომ ამ ნაწილაკების წარმოშობის დადგენაში გვეხმარება: ნაწილაკები რომელიღაც შუალედური არასტაბილური ნაწილაკის დაშლით გაჩნდნენ თუ სხვა პროცსების შედეგად. პირველ შემთხვევაში მათი ინვარიანტული მასა დაახლოებით ამ არასტაბილური ნაწილაკის მასის ტოლია, ხოლო მეორე შემთხვევაში განსხვავებულია. სწორედ ამ ხერხის საშუალებით შეგვიძლია სწრაფად მიმავალ მოვლენაში არასტაბილური ნაწილაკის დანახვა და სხვადასხვა ტიპის მოვლენათა ერთმანეთისგან გამოყოფა.
ავიღოთ უკვე კარგად გახმაურებული მაგალითი: დიდ ადრონულ კოლაიდერზე ჰიგზის ბოზონის ძებნა მისი ორ ფოტონად დაშლით. თუ ჰიგსი შეჯახებაში იბადება, ის ორ ფოტონად შეიძლება დაიშალოს(2. მარცხნივ). თუმცა ფოტონთა იგივე წყვილი თავისთავადაც შეიძლება გაჩნდეს, ყოველგვარი შუალედური ნაწილაკების გარეშე, უბრალოდ, კვარკების მიერ ფოტონების გამოსხივებით(2. მარჯვნივ). ფოტონთა წყვილს დეტექტორი ორივე შემთხვევაში დაინახავს, თუმცა ვერ გვეტყვის, რის ხარჯზე გაჩნდნენ ისინი. ფოტონების უბრალო დეტექტირებით ვერ ვიტყვით, რომ ზოგჯერ, ნამდვილად ჰიგსის ბოზონის გაჩენა და დაშლა ხდება.
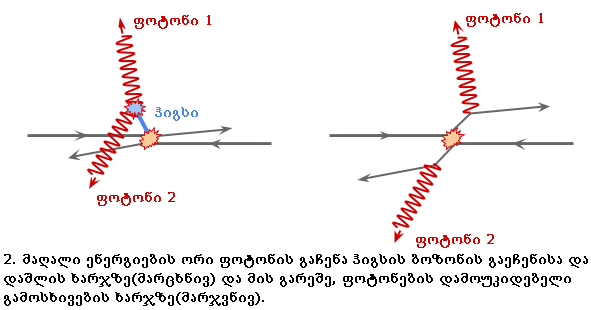
ასეთ შემთხვევაში ჩვენს დასახმარებლად ორი ფოტონის ინვარიანტული მასა mγγ მოდის. ყოველ კონკრეტულ მოვლენაში ორი ფოტონით, ამ ინვარიანტული მასის გამოთვლაა საჭირო, შემდეგ კი დათვლა, რამდენი მოვლენა, რამდენი ინვარიანტული მასით მივიღეთ, მერე კი გრაფიკი უნდა შევადგინოთ: მოვლენათა რაოდენობა mγγ-დან გამომდინარე. თუ მონაცემებში ჰიგსი არის, გრაფიკზე ამოზნექილობა გაჩნდება. ეს ის დამატებითი მოვლენებია, რომლებიც სწორედ ჰიგსის ბოზონის გაჩენითა და მისი ორ ფოტონად დაშლით მიიღება. გრაფიკზე ეს ამოზნექილობა ბოზონის მასას გვიჩვენებს, ხოლო მისი სიმაღლე, პროცესის ინტენსიურობას.
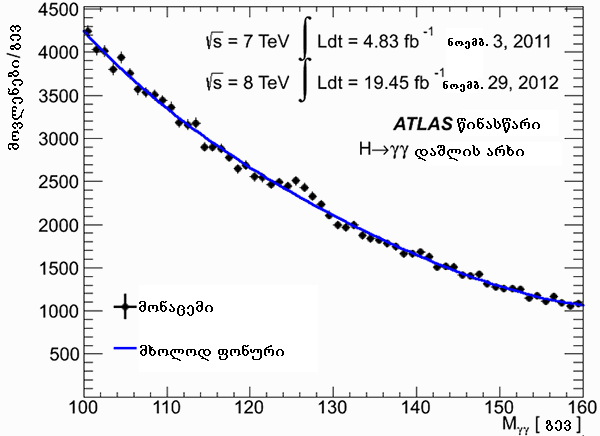
მესამე ნახაზზე, დეტექტორ ATLAS-ზე 2011-12 წლებში მიღებული მონაცემებია ორი ფოტონის ინვარიანტული მასების მონაკვეთისა 100 და 160 გიგაელექტრონვოლტზე(გევ). ჩანს ასე თუ ისე მდორე ფონი, რომელიც mγγ-ის მატებასთან ერთად იკლებს. ამ ფონზე კარგად შესამჩნევი ბორცვი ჩანს 125 გევ-ის რაიონში. ის ძალიან ძლიერი არ არის, თუმცა მცირე ცდომილებების ხარჯზე მას დიდი სტატისტიკური მნიშვნელობა აქვს, ანუ, ახალი ნაწილაკის არსებობა, რომელიც ორ ფოტონად იშლება, ექსპერიმენტით დადასტურებულად შეგვიძლია ჩავთვალოთ(შეკითხვები ჰიგსის ბოზონთან დაკავშირებით)(ექვივალენტობის პრინციპი).

ამონარიტი სტატიიდან (მოწვავთ რა ადგილიცაა)- ,,პოპულარულ გამოცემებში ამ სიდიდეს ”უძრაობის მასას” უწოდებენ და ”რელატივისტრუ მასას” უპირისპირებენ, თუმცა, კიდევ ერთხელ ავღნიშნოთ: ასეთი დაყოფა მხოლოდ პოპულარულ მასალებსა და ფიზიკის ზოგიერთ კურსებში ხდება. თანამედროვე ფიზიკაში არანაირი ”რელატივისტური მასა” არ არსებობს.” – აქ ყველაფერია ნათქვამი. საქართველოს ასტრონომიის მოყვარულთა ჯგუფს ფიზიკის საფუძვლიანი მცოდნე და საღად მოაზროვნე სჭირდება. ეს ჩემგან უფასო რჩევა.
p.s ღმერთმა უწყის კიდევ რამდენი ,,ფაქტობრივი” შეცდომაა ამ და სხვა სტატიებში.
კი, ჭირდება. იქნებ თქვენ დაგვეხმაროთ? ოღონდ უფულოები ვართ, იცოდეთ.