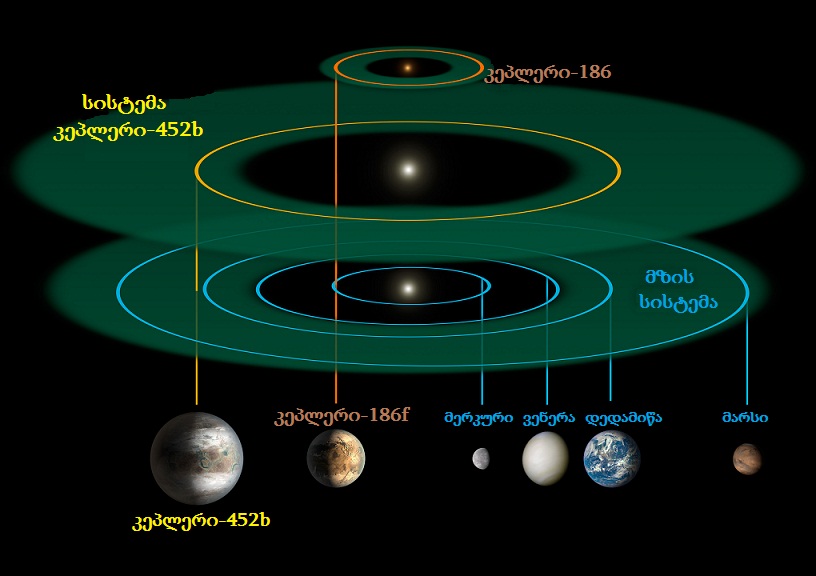
Posted by მოგეხსენებათ, NASA-ს მისიამ – ” კეპლერი”, კიდევ ერთი ეგზოპლანეტა აღმოაჩინა, რომელიც სიცოცხლისთვის ვარგის ზონაში იმყოფება, ანუ ის, მისი დედავარსკვლავიდან ისეთი მანძილით არის დაშორებული, რომ მასზე თხევადი წყლის არსებობისთვის ხელსაყრელი ტემპერატურაა. პლანეტა 1400 სინათლის წლითაა ჩვენგან დაშორებული და მზის მსგავსი, G2 ტიპის ვარსკვლავის გარშემო ბრუნავს. მას კეპლერ-452b უწოდეს, მეტსახელიც შეარქვეს — „დედამიწა 2.0“ და დედამიწის „ბიძაშვილადაც“ კი მონათლეს. ამ აღმოჩენით, დედამიწის მსგავსი ცბონილი ეგზოპლანეტების რიცხვი, სადაც შესაძლებელია სიცოცხლე არსებობდეს, 1030-მდე გაიზარდა, თუმცა კეპლერ-452b იმით არის გამორჩეული, რომ ის ყველაზე ახლოსაა დედამიწის ზომებთან და დედამიწაზე 60%-ით დიდია, ანუ დღემდე აღმოჩენილებს შორის ყველაზე პატარაა.
ამ აღმოჩენასთან დაკავშირებით, მსჯელობა და მითქმა-მოთქმა სოციალურ ქსელში არ წყდება. ერთის მხრივ, სასიამოვნოა, რომ მეცნიერებით ამდენი ადამიანია დაინტერესებული, თუმცა მეორეს მხრივ, არც ისე სასიამოვნოა, როცა საზოგადოებას ზოგიერთი რამ დამახინჯებულად ესმის, რაც ისეთ ვერსიებსა და შეთქმულების თეორიებს ბადებს, როგორიცაა: „ნასა გვატყუებს“, „კიბოს წამალი გამოგონებულია, მაგრამ მასზე მარტო მცირე ჯგუფს მიუწვდება ხელი“, „ვაქცინაცია გლობალური აფიორაა, რომელსაც ტრანსნაციონალური ფარმაცევტული კომპანიები იყენებენ ფულის გასაკეთებლად“, „დაავადებებს ხელოვნურად ქმნიან და ავრცელებენ, რომ პრეპარატები გაყიდონ“ და ა. შ.
ვინაიდან მჯერა, რომ მეცნიერულად უკეთესად განათლებული საზოგადოება ტექნოლოგიური, ეკონომიკური და სოციალური პროგრესის წინაპირობაა, თავს ვალდებულად ვთვლი, რამდენიმე გაუგებრობა ავხსნა.
1. ”თითქმის 9 წლიანი მოგზაურობის შემდეგ „ნიუ ჰორაიზონსმა“(”ახალი ჰორიზონტები”) როგორც იქნა პლუტონის ფოტოები გადაიღო და დედამიწაზე გადმოსცა, ათასობით სინათლის წლით დაშორებული პლანეტების სურათებს როგორღა იღებენ? გვატყუებს NASA”.
სურათი, რომელიც იხილეთ არ არის რეალური სურათი და არის მხატვრის წარმოსახვა. მსგავს მეთოდებს პრესსამსახურები ხშირად იყენებენ სტატიების გასაფორმებლად და მკითხველთა დასაინტერესებლად. რაც შეეხება პლანეტების ძებნის მეთოდს, კეპლერის მისია პლანეტებს ტრანზიტული მეთოდის საშუალებით ეძებს. როდესაც პლანეტა, ვარსკვლავის წინ ჩაივლის, ვარსკვლავის სიკაშკაშე მცირდება. ამ ცვლილების საშუალებით შესაძლებელია პლანეტის ზომის განსაზღვრა. თუ ეს მოვლენა რეგულარულად მეორდება დროის თანაბარ პერიოდებში, ესე იგი, ეს ნამდვილად პლანეტაა. ბრუნვის პერიოდის მიხედვით კი პლანეტის ორბიტის ზომა და მისი ზედაპირის საშუალო ტემპერატურა შეიძლება განისაზღვროს.
2. „თუ სინათლის სიჩქარით ვიმოძრავებთ, კეპლერ-452b-მდე მისაღწევად 1400 წელი დაგვჭირდება, რადგან ის 1400 სინათლის წლითაა დაშორებული, რაც იმას ნიშნავს, რომ მისგან წამოსულ სინათლეს 1400 წელი სჭირდება ჩვენამდე მოსაღწევად. შესაბამისად, ყველაფერი, რაც სინათლის სიჩქარით მოძრაობს იქამდე მისვლას 1400 წელს მოანდომებს.“
სინათლის სიჩქარე მართლაც არის სამყაროში არსებული ზღვრული სიჩქარე, თუმცა რელატივისტური ეფექტებიდან გამომდინარე, თუ მე 0,9999999c სიჩქარით ვიმოძრავებ (c აღნიშნავს სინათლის სიჩქარეს, ანუ 300 000 კმ/წმ.), იქ მისასვლელად, დაახლოებით 0,63 წელი, ანუ 7,5 თვე დამჭირდება. ეს არ ნიშნავს იმას, რომ მე სინათლის სიჩქარეზე სწრაფად ვიმოძრავე, უბრალოდ მანძილი რომელიც გავიარე მოძრაობის მიმართულებით შეიკუმშა და, ჩემი პერსპექტივიდან, მე 0,63 სინათლის წელი გავიარე 0,63 წელში, როდესაც დედამიწაზე არსებული დამკვირვებელი დაინახავს (თუ იქამდე იცოცხლა), რომ მე 1400 წელი დამჭირდა 1400 სინათლის წლის დასაფარად და ჩემთვის დრო ნელა გადიოდა. მაშასადამე, თუ ჩვენ ასეთ მისიაში გავუშვებთ ვინმეს იმისთვის, რომ ფოტო ჩამოგვიტანოს, ჩვენი პერსპექტივიდან, მას მინიმუმ 2800 (1400 წელი მისასვლელად და ამდენივე დაბრუნებისთვის) წელი დასჭირდება; შესაბამისად, სინათლის სიჩქარე ურთიერთქმედების ან იმფორმაციის (პრაგმატული თვალსაზრისით, გადაღებული ფოტოს) გადაცემის ზღვრული სიჩქარეა და ასეთი მისიით ჩვენც და მისიის მონაწილეც უფრო მეტად წავაგებთ, ვიდრე მოვიგებთ, რაც, სავარაუდოდ, მიზეზია იმისა, თუ რატომ არ არის ამ იდეაზე სამეცნიერო ფანტასტიკის ჟანრის ბევრი ნოველა დაწერილი(თუმცა ლარი ნივენის „A World Out of Time“ ერთ-ერთი გამონაკლისია).
3. „ვინაიდან ეს პლანეტა 1,6-ჯერ (60%-ით) დიდია დედამიწაზე, მისი გრავიტაცია 1,6-ჯერ ძლიერია, შესაბამისად, მასზე თქვენი მასა 1,6-ჯერ გაიზრდება.“
ამ ტექსტში ორი გაუგებრობაა. პირველი ის, რომ მასა გრავიტაციაზე დამოკიდებული არ არის, შესაბამისად, ის იგივე დარჩება, ხოლო წონა გაიზრდება, რადგან კონკრეტული მასის მქონე სხეულის წონა ლოკალურ თავისუფალი ვარდნის აჩქარებაზეა დამოკიდებული და ნიუტონებში(ნ) იზომება (და არა კილოგრამებში; გრამი, კილოგრამი, ტონა, ფუნტი და ა. შ. მასის საზომი ერთეულებია). წონის გამოსათვლელად შეგვიძლია გამოვიყენოთ შემდეგი ფორმულა W = mg (სადაც W სხეულის წონაა, m — ამავე სხეულის მასა, ხოლო g ლოკალური თავისუფალი ვარდნის აჩქარება).
დედამიწაზე თავისუფალი ვარდნის აჩქარება არის დაახლოებით 9,8 მ/წმ², ანუ, მაგალითსითვის, 10 კგ. მასის მქონე სხეულის წონა დედამიწაზე არის 10 × 9,8 ნ, რაც 98 ნ-ს უდრის.
მეორე გაუგებრობა ეხება სხეულის წონის დამოკიდებულებას პლანეტის გრავიტაციული ველის სიძლიერეზე. მიუხედავად იმისა, რომ პლანეტის (ისევე, როგორც ნებისმიერი სხეულის) გრავიტაციული ველის სიძლიერე ამ პლანეტის მასის პროპორციულია, თავისუფალი ვარდნის აჩქარების გამოთვლისას გასათვალისწინებელია მისი მეორე მახასიათებელი — რადიუსი. თავისუფალი ვარდნის აჩქარების დამოკიდებულება პლანეტის მასასა და რადიუსზე გამოისახება შემდეგი ფორმულით: g = GM / r² (სადაც g თავისუფალი ვარდნის აჩქარებაა, G — გრავიტაციული მუდმივა, ანუ დაახლოებით 6,67 × 10–¹¹ ნ·მ²/კგ², M — პლანეტის მასა, ხოლო r — პლანეტის რადიუსი). ეს იმ შემთხვევაში, თუ პლანეტის ზედაპირზე ან ზედაპირთან საკმაოდ ახლოსაა სხეული; თუ ზედაპირზე მაღლაა, r აღნიშნავს პლანეტის რადიუსისა და მისი ზედაპირიდან სხეულის სიმაღლის ჯამს, სხვანაირად რომ ვთქვათ, სხეულის (სხეულის ცენტრის) დაშორებას პლანეტის ცენტრიდან, ანუ r = R + h (სადაც r არის პლანეტისა და სხეულის ცენტრებს შორის მანძილი, R — პლანეტის რადიუსი, ხოლო h — სხეულის სიმაღლე პლანეტის ზედაპირიდან). ეს ყველაფერი მხოლოდ იმ შემთხვევაში, თუ პლანეტა სფერულია და სიმკვრივის მიხედვით ასე თუ ისე ერთგვაროვანია ან სიმკვრივე იზრდება / მცირდება (რატომ უნდა მცირდებოდეს, მაგრამ მაინც) ცენტრისკენ (შრეების მიხედვით).
თუ დავუშვებთ, რომ კეპლერ-452b სფერულია (უნდა იყოს, რადგან საკმაოდ დიდია), მისი ქანების სიმკვრივე იზრდება ცენტრისკენ და მისი საშუალო სიმკვრივე დედამიწის სიმკვრივის ტოლია, შეგვიძლია გამოვთვალოთ მასზე წონის ზრდის რეალური ფაქტორი დედამიწის მიმართ: ჯერ გამოვთვალოთ კეპლერ-452b-ს მასის ფაქტორი დედამიწის მასის მიმართ. ვინაიდან სხეულის მასის მის მოცულობახე და სიმკვრივეზე დამოკიდებულება გამოისახება ფორმულით m = Vρ, დამოკიდებულება წრფივია, ანუ მასის ფაქტორი იგივე იქნება, რაც მოცულობის და ვინაიდან კეპლერ-452b დედამიწას მოცულობით 1,6-ჯერ აღემატება, მისი მასაც დედამიწისას 1,6-ჯერ უნდა აღემატებოდეს.
ახლა გამოვთვალოთ კეპლერ-452b-ს რადიუსის ფაქტორი დედამიწის რადიუსის მიმართ. იქედან გამომდინარე, რომ სფეროს რადიუსის მის მოცულობაზე დამოკიდებულება გამოისახება, ფორმულით r = ∛(¾V / π) (სადაც r სფეროს რადიუსია, V — ამავე სფეროს მოცულობა, π — წრის კონსტანტა, ანუ დაახლოებით 3,14), დამოკიდებულება კუბური ფესვის შესაბამისია და ვინაიდან კეპლერ-452b-ს მოცულობა დედამიწის მოცულობაზე 1,6-ჯერ მეტია, რადიუსის ფაქტორი იქნება ∛(1,6) (რადგანაც დანარჩენი წევრები იკვეცება), რაც დაახლოებით 1,17-ს უდრის.
ბოლოს, გამოვთვალოთ კეპლერ-452b-ს თავისუფალი ვარდნის აჩქარების ფაქტორი დედამიწის თავისუფალი ვარდნის აჩქარების მიმართ. რადგან თავისუფალი ვარდნის აჩქარების დამოკიდებულება პლანეტის მასასა რადიუსზე გამოისახება ფორმულით g = GM / r² და რადგან კეპლერ-452b დედამიწას მასით — 1,6-ჯერ, ხოლო რადიუსით 1,17-ჯერ აღემატება, თავისუფალი ვარდნის აჩქარების ფაქტორი იქნება 1,6 / 1,17², (რადგანაც G იკვეცება), ანუ დაახლოებით 1,6 / 1,37, რაც დაახლოებით 1,17-ს უდრის. ვინაიდან წონის დამოკიდებულება თავისუფალი ვარდნის აჩქარებაზე და მასაზე გამოისახება ფორმულით W = mg, დამოკიდებულება წრფივია, ანუ წონის ფაქტორი იგივე იქნება, რაც თავისუფალი ვარდნის აჩქარების (რადგან m იკვეცება). ასე რომ, თუ ის პლანეტა აგებულებით დედამიწის მსგავსია, მასზე თქვენი წონა (და არა მასა) დაახლოებით 1,17-ჯერ გაიზრდება (და არა 1,6-ჯერ).
ავტორი: გიორგი გზირიშვილი(სტუდენტი).