Posted by ექსპერიმენტი, რომელმაც სინათლის ბუნების შესახებ წარმოდგენა შეგვიცვალა, ძალიან მარტივია. ის ”ყველგან შეიძლება გავიმეოროთ, სადაც მზე ანათებს”, ამბობდა ინგლისელი ფიზიკოსი თომას იუნგი, 1803 წლის ნოემბერში, როცა სამეფო საზოგადოების წევრების წინაშე ე.წ. ორმაგი ჭრილის ექსპერიმენტის დემონსტრირებას ახდენდა. მან საკმაოდ ელეგანტური და კარგად გააზრებული ექსპერიმენტი მოიგონა, რომელიც სინათლის ტალღურ ბუნებას გვიჩვენებდა. დიდი ისააკ ნიუტონის თეორია კი გვეუბნებოდა, რომ სინათლე კორპუსკულების, ანუ ნაწილაკების ნაკადია (ერთიც არის და მეორეც ერთდროულად).
წინა საუკუნის დასაწყისში გაჩენილი კვანტური ფიზიკა კი სინათლეს (იგივე, ელექტრომაგნიტური გამოსხივება), უმცირესი განუყოფელი ერთეულებისგან, ენერგიის კვანტებისგან– ფოტონებისგან შემდგარ ნაკადად წარმოგვიდგენს. იუნგის ექსპერიმენტი, ერთეული ფოტონის ან მატერიის ცალკეული ნაწილაკების გამოყენებით – ელექტრონი, ნეიტრონი, გამოცანას წარმოადგენს, რომელიც თვით რეალობის ბუნებაზე დაგვაფიქრებს. ზოგიერთის მტკიცებით, ადამიანის გონიც კი ზემოქმედებს კვანტურ სამყაროზე. მარტივი ექსპერიმენტით თუ არის შესაძლებელი ამის დემონსტრირება?
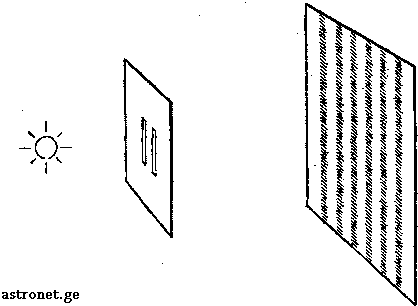თუ ელექტრონებს დამუხტული ბურთულების სახით წარმოვიდგენთ, მაშინ ორ ვიწრო ჭრილში გასულმა ასეთმა ბურთულებმა, მოპირდაპირე მხარეს მდებარე ეკრანზე ამ ჭრილების ფორმის ზოლები უნდა დახატოს. სინამდვილეში კი ეკრანზე გაცილებით რთული ჩუქურთმების მქონე ბნელი და ნათელი ზოლების მიმდევრობას დავინახავთ. საქმე იმაშია, რომ ჭრილებში გასვლისას ელექტრონები ნაწილაკებივითაც იქცევიან და ტალღებივითაც (ეს სხვა ელემენტარულ ნაწილაკებსაც ეხება) (მოკლედ ელემენტარული ნაწილაკების შესახებ).
ეს ექსპერიმენტი არც მაშინ იცვლის სახეს, როცა ჭრილებში ცალკეული ელექტრონები გადიან – ერთ ნაწილაკსაც კი შეუძლია იყოს ტალღა და ერთდროულად ორ ჭრილში გავიდეს. მიკროსამყაროს ობიექტთა ამ უცნაურ თვისებას კვანტურ-ტალღური დუალიზმი ეწოდება.
მათემატიკის ენით რომ ვთქვათ, ჭრილებში არა ფიზიკური ნაწილაკი გადის, არამედ ფიზიკური ტალღა, ე.წ. ტალღური ფუნქცია – აბსტრაქტული მათემატიკური ფუნქცია, რომელიც ფოტონის მგდომარეობას გვიჩვენებს (ამ შემთხვევაში – მდებარეობას). ტალღური ფუნქცია ტალღასავით იქცევა. ის ორივე ჭრილს ხვდება და სხვა ტალღების სახით გადის მეორე მხარეს, გავრცელებითა და ურთიერთ ინტენფერენციით (ურთიერთ გაძლიერება, ჩახშობა). ტალღური ფუნქციით შეგვიძლია გავიგოთ ალბათობა იმისა, თუ სად შეიძლება მდებარეობდეს ფოტონი.
იქ, სადაც ტალღური ფუნქციები კონსტრუქციულად ინტერფერირებს, ფოტონის მდებარეობის მეტი ალბათობა იქნება და პირიქით, სადაც ინტენფერენცია დესტრუქციულია, ფოტონის იქ მდებარეობის ალბათობაც მცირეა. გაზომვა, ამ შემთხვევაში, ტალღური ფუნქციის ურთიერთქმედებაა დეტექტორთან, რაც ფუნქციის რღვევას იწვევს. შედეგად, ის გვიჩვენებს ერთ-ერთ ადგილს, რომელზეც ფოტონის მატერიალიზება მოხდა.
კვანტური მექანიკისთვის, ტალღური ფუნქციის აშკარა კოლაფსი უამრავი კონცეპტუალური სირთულეების წყაროდ იქცა. კოლაფსამდე ვერავინ იტყვის, ზუსტად სად აღმოჩნდება ფოტონი; ის ნებისმიერ ადგილზე შეიძლება იყოს არანულოვანი ალბათობით. არ არსებობს საშუალება, რომლითაც წყაროდან დეტექტორისკენ მოძრავი ფოტონის ზუსტი ტრაექტორია შეიძლება დადგინდეს. ფოტონი არარეალურია იმ თვალსაზრისით, რომლითაც რეალურია თვითმფრინავი, მოძრავი A წერტილიდან B წერტილისკენ.
ვერნერ ჰაიზენბერგი, სხვათა შორის, ამ მათემატიკის შემდეგნაირ ინტერპრეტირებას ახდენდა – რეალობა მაშინ არსებობს, როცა ის დაიმზირება. ”ობიექტურ-რეალური სამყაროს იდეა, რომლის უმცირესი ნაწილაკები იმ თვალსაზრისითვე ობიექტურად არსებობენ, როგორც ქვები და ხეები, მიუხედავად იმისა, ვახდენთ თუ არა მათზე დაკვირვებას – შეუძლებელია”, ამბობდა ჰაიზენბერგი. ჯონ უაილერიც ამავე ექსპერიმენტზე დაყრდნობით ამბობდა, რომ ”ელემენტარული კვანტური მოვლენა მხოლოდ მაშინ ჩაითვლება მოვლენად, როცა მოხდება მისი რეგისტრიება” (მთვარე მაშინ არსებობს, როცა ვუყურებთ?).
ორმაგი ჭრილის ექსპერიმენტის განსხვავებული ინტერპრეტაციებიც არსებობს. მაგალითად, დე ბროილ-ბომის თეორია – რეალობა ტალღაც არის და ნაწილაკიც. ტრაექტორია ყველა ფოტონს აქვს. ის პილოტურ ტალღაზე გადის, რომელიც ორივე ჭრილში აღწევს, ინტერფერირებს და ფოტონს კონსტრუქციული ინტენფერენციისკენ მიმართავს.
1979 წელს, ქრის დიუდნიმ და მისმა კოლეგებმა (კოლეჯი ბრიკბექი, ლონდონი), ამ თეორიით ნავარაუდევი მოდელირება მოახდინეს ტრაექტორიებისა, რომლებიც ორმაგ ჭრილში გადის. უკანასკნელი ათი წლის განმვლობაში, ექსპერიმენტატორებმა დაადგინეს, რომ ასეთი ტრაექტორიები არსებობს, თუმცა იყენებდნენ ე.წ. სუსტი გაზომვის მეთოდებს. საკამათოა, მაგრამ ექსპერიმენტებმა გვიჩვენა, რომ დე ბროილ-ბომის თეორიას კვანტური სამყაროს ქცევის ახსნა ჯერ კიდევ შეუძლია.
რაც მთავარია, არ არის საჭირო დამკვირვებელი, გაზომვები , ან რაღაც არამატერიალური გონი.
ამ თეორიის გადასამოწმებლად, ვენის უნივერსიტეტის მეცნიერები სულ უფრო დიდ მოლეკულებს აგზავნიდნენ ჭრილებისკენ. ფუნქციის კოლაფსის თეორია წინასწარმეტყველებს, რომ გარკვეული ზღვრის მერე, მატერიის ფრაგმენტები კვანტურ (სუპერპოზიციის) თვისებებს კარგავენ, ორივე ჭრილში ერთდროულად აღარ გადიან და ინტენფერენციული სურათიც აღარ მიიღება. ჭრილისკენ გაგზავნილი იქნა 800 ატომისგან შემდგარი მოლეკულა, რამაც მაინც ინტენფერენციული სურათი მოგვცა. ზღვრის დადგენა გრძელდება.
როჯერ პენროუზს კოლაფსის თეორიის საკუთარი ვერსია ჰქონდა – რაც უფრო დიდია სუპერპოზიციაში მყოფი ობიექტის მასა, მით უფრო მალე კოლაფსირებს ერთი ან მეორე მდგომარეობისკენ გრავიტაციული არასტაბილურობების გამო (ჭრილის მასა)…. არც აქ არის აუცილებელი დამკვირვებელი ან გონი. პენროუზის იდეის შემოწმებაზე, ორმაგი ჭრილის ექსპერიმენტის ერთ-ერთი ვერსიით, დიკ ბოუმეესთერი მუშოაბს (კალიფორნიის უნივერსიტეტი, სანტა ბარბარა, ა.შ.შ.).
ნებისმიერ შემთხვევაში, ეს ექსპერიმენტები გვიჩვენებს, რომ რეალობის ბუნებაზე დარწმუნებით ვერ ვისაუბრებთ, რაც არ უნდა მტკიცე მეთამატიკური ან ფილოსოფიური მოსაზრებები უმაგრებდეს ზურგს. იმასაც თუ გავითვალსიწინებთ, რომ ნეირობიოლოგები და ფილოსოფოსები გონის რაობის შესახებ ერთ აზრზე ვერ ჩამოყალიბებულან, ნაჩქარევი ან მცდარი იქნება მტკიცებულება იმისა, რომ ის, ტალღური ფუნქციის კოლაფსს იწვევს (რეალობის კვანტური ილუზია).